The True score MTMM model
The true score MTMM model was developed in order to decompose the quality of a question in two components: the reliability and the validity. This makes sense if one wants to study these two characteristics of questions because different factors may determine the reliability than the validity.
This decomposition can be made by a different parameterization of the Classical MTMM model. Now the basic structure of the model is split in two parts by introducing the so-called true score (t) which is equal to the observed variable except for the random errors. So the first equation is as in the classical test theory (Lord and Novick 1956):
$Y = t + e$ (1)
The second equation specifies the relationship between the true score ($t$), the latent traits ($F$) and the systematic errors related to the method used:
$t = a + b F + M$ (2)
Standardizing these two equations we get:
$Y = r t + e$ (3)
and
$t = v F + m M$ (4)
In equation (3) $r$ is the strength of the relationship between the true score and the observed variable. In the literature $r^{2}$ is the reliability of the observed variable which is equal to $1 - var(e)$.
In equation (4) the coefficient $v$ indicates the strength of relationship between the latent trait and the true score ($t$) and $v^{2}$ is called the validity of the observed variable.
The coefficient $m$ is called the method effect and since $var(t)=var(F)=var(M)=1$ it follows that $v^{2}=1-m^{2}$. This means that they are each other's complement.
If the model specified in (1) and (2) or in (3) and (4) can be estimated we see that we get a separate estimate of the reliability coefficient ($r$) and the validity coefficient ($v$). This was not the case in the classical model although these two models are equivalent because the parameters in the two models can be derived from each other as will be show below.
Substituting equation (4) in (3) we get:
$Y = r v F + r m M + e$ (5)
The last equation shows that this equation is the same as the basic equation of the classical MTMM model with $q= rv$ and $s= r m$ while the $var(e)$ is the same in both MTMM models.
We see that $q^{2}$ what we have called before the quality of the questions is now equal to the product of the reliability and the validity ($r^{2}v^{2}$). We will continue to do so.
On the other hand we see that $s^{2}$ what was called the variance of the systematic error has been changed because it is equal to ($r^{2}m^{2}$). We prefer to use the coefficient $m$ for the method effect because it is pure estimate of the method effect and not the product of the method effect and the reliability coefficient.
With respect to the data collection nothing will be changed so the only difference is that we get a separate estimate of the reliability and validity and an estimate of the purer method effect.
On the data presented in the section about the classical MTMM approach we also can estimate the parameters of the True score MTMM model.
This decomposition can be made by a different parameterization of the Classical MTMM model. Now the basic structure of the model is split in two parts by introducing the so-called true score (t) which is equal to the observed variable except for the random errors. So the first equation is as in the classical test theory (Lord and Novick 1956):
$Y = t + e$ (1)
The second equation specifies the relationship between the true score ($t$), the latent traits ($F$) and the systematic errors related to the method used:
$t = a + b F + M$ (2)
Standardizing these two equations we get:
$Y = r t + e$ (3)
and
$t = v F + m M$ (4)
In equation (3) $r$ is the strength of the relationship between the true score and the observed variable. In the literature $r^{2}$ is the reliability of the observed variable which is equal to $1 - var(e)$.
In equation (4) the coefficient $v$ indicates the strength of relationship between the latent trait and the true score ($t$) and $v^{2}$ is called the validity of the observed variable.
The coefficient $m$ is called the method effect and since $var(t)=var(F)=var(M)=1$ it follows that $v^{2}=1-m^{2}$. This means that they are each other's complement.
If the model specified in (1) and (2) or in (3) and (4) can be estimated we see that we get a separate estimate of the reliability coefficient ($r$) and the validity coefficient ($v$). This was not the case in the classical model although these two models are equivalent because the parameters in the two models can be derived from each other as will be show below.
Substituting equation (4) in (3) we get:
$Y = r v F + r m M + e$ (5)
The last equation shows that this equation is the same as the basic equation of the classical MTMM model with $q= rv$ and $s= r m$ while the $var(e)$ is the same in both MTMM models.
We see that $q^{2}$ what we have called before the quality of the questions is now equal to the product of the reliability and the validity ($r^{2}v^{2}$). We will continue to do so.
On the other hand we see that $s^{2}$ what was called the variance of the systematic error has been changed because it is equal to ($r^{2}m^{2}$). We prefer to use the coefficient $m$ for the method effect because it is pure estimate of the method effect and not the product of the method effect and the reliability coefficient.
With respect to the data collection nothing will be changed so the only difference is that we get a separate estimate of the reliability and validity and an estimate of the purer method effect.
On the data presented in the section about the classical MTMM approach we also can estimate the parameters of the True score MTMM model.
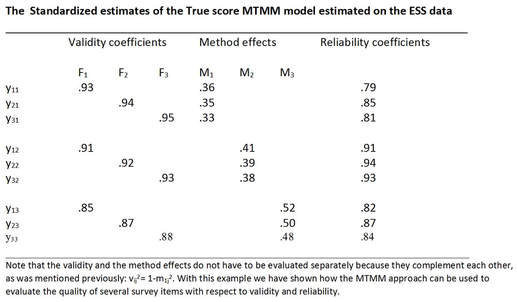
It can be checked that the quality coefficients of the classical model are equal to the product of the reliability and validity coefficients in this model except for rounding-off errors. There we concluded that method 2 was better with respect to all three questions. Using the True score model we see that this is not true for the validity coefficients. In that respect the first method is a bit better but the better quality of the method 2 comes from the reliability which is quite a bit higher for method 2 than for the other two methods.
It is form this more detailed information that Saris and Andrews have introduced the True score model for the analysis of data of MTMM experiments.
It is form this more detailed information that Saris and Andrews have introduced the True score model for the analysis of data of MTMM experiments.
References:
Saris W. E., and F. M. Andrews 1991. Evaluation of measurement instruments using a structural modeling approach. In P. P. Biemer, R. M. Groves, L. E. Lyberg, N. Mathiowetz and S. Sudman (eds.), Measurement Errors in Surveys, New York: Wiley, 575─599.
Saris W. E., and C. Aalberts 2003. Different explanations for correlated errors in MTMM studies. Structural Equation Modeling, 10, 193─214.
Saris W.E. and I.N.Gallhofer (2014) Design, evaluation and analysis of questionnaires for survey research. Hoboken, Wiley, (chapter 9 and 10)
Saris W. E., and F. M. Andrews 1991. Evaluation of measurement instruments using a structural modeling approach. In P. P. Biemer, R. M. Groves, L. E. Lyberg, N. Mathiowetz and S. Sudman (eds.), Measurement Errors in Surveys, New York: Wiley, 575─599.
Saris W. E., and C. Aalberts 2003. Different explanations for correlated errors in MTMM studies. Structural Equation Modeling, 10, 193─214.
Saris W.E. and I.N.Gallhofer (2014) Design, evaluation and analysis of questionnaires for survey research. Hoboken, Wiley, (chapter 9 and 10)