Two statistics to detect misspecifications: MI and EPC
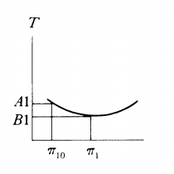Figure 1 The relation between a parameter and the test statistic T
Instead of testing models as a whole one can also concentrate on single parameters in a larger model. It would be attractive to have a procedures that could provide information about possible misspecifications of parameters in the same analysis when the model is estimated.
The first statistic developed by Sörbom (1975) for this purpose was the Modification Index (MI). In figure 1 at the side, the argument for this statistic has been given. The curve presents the values of the test statistic (T) for different values of the parameter. A1 presents the value of T for a specific fixed or restricted parameter. For this value the function does no obtain its optimal value. The minimum of the function is obtained when T = B1. This means that A1-B1 is the improvement in the test statistic when the parameter value moves to the value that optimizes the value of the test statistic T. Based on this idea the modification index (MI) is defined as
MI = A1 –B1 (1)
So MI is the improvement in the test statistic that is possible if a restricted parameter is adjusted so that the test statistic obtains its optimal value. This statistic can be computed for all restricted parameters at the same time that the model is estimated. For the statistical details we refer to Sörbom (1975).
The first statistic developed by Sörbom (1975) for this purpose was the Modification Index (MI). In figure 1 at the side, the argument for this statistic has been given. The curve presents the values of the test statistic (T) for different values of the parameter. A1 presents the value of T for a specific fixed or restricted parameter. For this value the function does no obtain its optimal value. The minimum of the function is obtained when T = B1. This means that A1-B1 is the improvement in the test statistic when the parameter value moves to the value that optimizes the value of the test statistic T. Based on this idea the modification index (MI) is defined as
MI = A1 –B1 (1)
So MI is the improvement in the test statistic that is possible if a restricted parameter is adjusted so that the test statistic obtains its optimal value. This statistic can be computed for all restricted parameters at the same time that the model is estimated. For the statistical details we refer to Sörbom (1975).
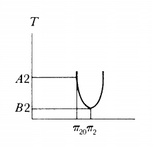Figure 2 The relationships between another parameter and the test statistic
Saris and Satorra (1987) have criticized the use of this statistic for the rather obvious reason that can be illustrated by comparing figure 1 with figure 2.
The idea behind figure 2 is the same as for Figure 1. The difference is that the change in the test statistic T in Figure 2 is much steeper than in Figure 1. As a consequence of this the MI in figure 1 is much smaller than in Figure 2.
On the other hand, the change in the values of the parameter of interest is much larger in Figure 1 than in Figure 2.
So an alternative statistic would be the “expected parameter change” or EPC which is:
The idea behind figure 2 is the same as for Figure 1. The difference is that the change in the test statistic T in Figure 2 is much steeper than in Figure 1. As a consequence of this the MI in figure 1 is much smaller than in Figure 2.
On the other hand, the change in the values of the parameter of interest is much larger in Figure 1 than in Figure 2.
So an alternative statistic would be the “expected parameter change” or EPC which is:
EPC= πio-πi (2)
Also this statistic can be estimated at the same time when the model is estimated. For the statistical details we refer to the paper of Saris, Satorra and Sörbom (1987).
Because one is mainly interested in the values of the parameters it seems much more attractive to concentrate on the EPC than on the MI. However one could also use both at the same time where MI is the test statistic that can indicate whether the EPC is a significant improvement in fit of the model. In the next section we present the basic tools of the test of misspecification of single parameters in structural equation models.
Because one is mainly interested in the values of the parameters it seems much more attractive to concentrate on the EPC than on the MI. However one could also use both at the same time where MI is the test statistic that can indicate whether the EPC is a significant improvement in fit of the model. In the next section we present the basic tools of the test of misspecification of single parameters in structural equation models.
