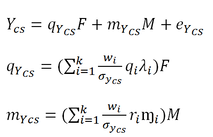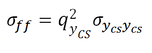The Quality of a Composite Score of a Concept with Reflective Indicators
Complex concepts with reflective indicators are latent variables that have an effect on different indicators of the latent variable. For example the latent variable “Job satisfaction” with the indicators such as” how satisfied are you with your job”, “how much do you like your job”, “Would you choose these job again”. The answers to these questions are determined by the latent variable Job satisfaction. A causal model, specified as a factor model can be used for the relationships. Normally a weighted sum score of the responses to the indicators is used as a measure for the latent variable.
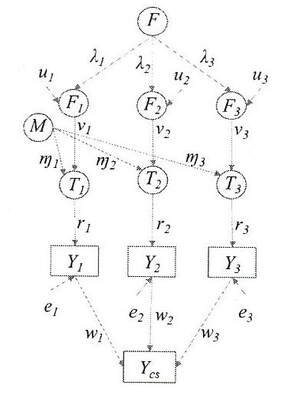
This situation is presented in the picture at the side. The observed answers to the three questions are represented by Y1, Y2, Y3. These observed responses contain errors. The composite score (Ycs) is the weighted sum of these three variables, therefore this composite score will also contain errors. So the question to answer is: how good is this composite score as measure for the complex concept satisfaction (F) given the indicators F1, F2, F3 and the systematic effects connected with the chosen method (M)?
Estimating the weights and the loadings
From SQP, or otherwise, one can get information about the quality coefficients ri, vi, mi, for all three or any number of single questions. That means that in the model only the effects of F on its indicators and the weights are unknown. However, the weights can be chosen to be 1 or unequal to 1, that is up to the researcher. Lawley and Maxwell (1971) have suggested an approach to determine the weights that maximize the quality (correlation) of the composite score for the complex concept. Given the weights the values of the composite score can be computed for all cases and the variance and standard deviation of these variables are also known. In order to take care that the composite score has a variance of 1 like all other variables, the chosen weights have to be divided by sycs which is the standard deviation of the composite score before standardization.
It can be shown that on the basis of the correlations between the observed variables Y1, Y2, Y3 the correlations between the latent variables F1, F2, F3 can be obtained.
This situation is presented in the picture at the side. The observed answers to the three questions are represented by Y1, Y2, Y3. These observed responses contain errors. The composite score (Ycs) is the weighted sum of these three variables, therefore this composite score will also contain errors. So the question to answer is: how good is this composite score as measure for the complex concept satisfaction (F) given the indicators F1, F2, F3 and the systematic effects connected with the chosen method (M)?
Estimating the weights and the loadings
From SQP, or otherwise, one can get information about the quality coefficients ri, vi, mi, for all three or any number of single questions. That means that in the model only the effects of F on its indicators and the weights are unknown. However, the weights can be chosen to be 1 or unequal to 1, that is up to the researcher. Lawley and Maxwell (1971) have suggested an approach to determine the weights that maximize the quality (correlation) of the composite score for the complex concept. Given the weights the values of the composite score can be computed for all cases and the variance and standard deviation of these variables are also known. In order to take care that the composite score has a variance of 1 like all other variables, the chosen weights have to be divided by sycs which is the standard deviation of the composite score before standardization.
It can be shown that on the basis of the correlations between the observed variables Y1, Y2, Y3 the correlations between the latent variables F1, F2, F3 can be obtained.
On the basis of these correlations the effects λi between the concept of interest and the indicators can be estimated if there are at least 3 indicators. If there are only two questions used the λ1 and λ2 can only be estimated assuming that these two coefficients are equal. Because the indicators will not all prefectly represent the complex variables of interest, we introduce also unique components (u1, u2, u3) for the indicators. They are another source of errors.
The quality of YCS
Given this specification of the model it follows
for all i because
or
qYcs = ∑i ri vi λi is the effect of F on Ycs
mYcs = ∑i ri mi is the systematic method effect on Ycs
The quality of the composite score as measure of F is equal to qYcs2
The variance of the unstandardized concept is presented below: Above two equations are wrong: Summation
see above i-k and the weight
see above i-k and the weight
The proofs of these results can be found in: Anna DeCastellarnau and Willem Saris Correcting correlation and covariance matrices for measurement errors before using SEM (obtainable from SRF).