between a complex and a simple concept

Correcting the correlation and covariance between a complex and a simple concept

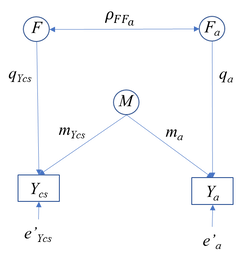
Next, we discuss the model where a complex concept measured by a composite score Y_cs shares the same method with an additional simple concept (F_a). Since we have derived in the a previous section the effect of the concept on interest (F) and the method M on the computed composite score of the complex variable F we can simplified this model as presented in the Figure below.

The simplified model of a complex concept and an additional simple concept where all variables are standardized

As we have seen for a similar model it can be proven that

ρ_{Y_csY_a} = q_{Y_cs} q_a ρ_FFa + m_{Y_cs}m_a

Which shows:

ρ_FFa = (ρ_{Y_csY_a} - m_{Y_cs} m_a ) / q_{Y_cs} q_a

In order to compute the covariance between a complex concept and a simple concept the correlation between the two variables has to be multiplied with the standard deviations of these variables corrected for measurement error. This means that

σ_FFa = σ_F ρ_FFa σ_Fa

For any complex concept the standard deviation is equal to q_{Y_cs}σ_{Y_cs} which was derived before.

For F_a the standard deviation has been derived to be equal to q_a σ_Ya

<< previous

next >>